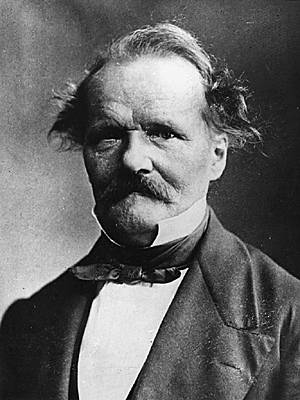On January 29, 1810, German mathematician Ernst Eduard Kummer was born. One of his major contributions is the introduction of ideal numbers, which are defined as a special subgroup of a ring. He extended the fundamental theorem of arithmetic to complex number fields.He also discovered the fourth order surface based on the singular surface of the quadratic line complex. This Kummer surface has 16 isolated conical double points and 16 singular tangent planes.
“A peculiar beauty reigns in the realm of mathematics, a beauty which resembles not so much the beauty of art as the beauty of nature and which affects the reflective mind, which has acquired an appreciation of it, very much like the latter. “
— Ernst Eduard Kummer [10]
Ernst Kummer – Youth and Education
Ernst Kummer was born in Sorau, Brandenburg (then part of Prussia)to his father Carl Gotthelf Kummer, a physician. However his father died when Ernst was only three years old and Ernst and his elder brother Karl were brought up by their mother. Ernst received private coaching before entering the Gymnasium in Sorau when he was nine years old. In 1828 Kummer entered the University of Halle to study Protestant theology. But fortunately for the good of mathematics, Kummer received mathematics teaching as part of his degree to provide a proper foundation to the study of philosophy. Soon the study of mathematics should become his main subject, although at this stage he still saw it as leading to a later study of philosophy.[1]
A School Teacher in the Berlin Academy
In 1831 Kummer was awarded a prize for a mathematical essay and in the same year he was awarded his certificate to enable him to teach in schools. Moreover, on the strength of his prize winning essay, he was awarded a doctorate. After a probationary year at the Gymnasium in Sorau where he had been educated, he was appointed to a teaching post at the Gymnasium in Liegnitz, now Legnica in Poland that he held for the next 10 years. Some of his pupils there had great ability, most prominent among them Leopold Kronecker, and conversely they were extremely fortunate to find a school teacher of Kummer‘s quality and ability to inspire. During Kummer‘s first period of mathematics he worked on function theory. He extended Gauss‘s work on hypergeometric series, giving developments that are useful in the theory of differential equations.[7] He was the first to compute the monodromy groups of these series. In 1839, although still a school teacher, Kummer was elected to the Berlin Academy on Dirichlet‘s recommendation.
Ideal Numbers
In 1842, Kummer became professor of mathematics at the University of Breslau (now Wrocław, Poland). In 1855 he succeeded Peter Gustav Lejeune Dirichlet [8] as professor of mathematics at the University of Berlin, at the same time also becoming a professor at the Berlin War College. In 1843, Kummer showed Dirichlet an attempted proof of Fermat’s last theorem. But, Dirichlet found an error, and Kummer continued his search and developed the concept of so-called ideal numbers. In number theory an ideal number is an algebraic integer which represents an ideal in the ring of integers of a number field. An ideal is a special subset of an algebraic ring. Ideals generalize certain subsets of the integers, such as the even numbers or the multiples of 3. Addition and subtraction of even numbers preserves evenness, and multiplying an even number by any other integer results in another even number.
Algebraic Numbers
Using the concept of ideal numbers, Ernst Kummer proved the insolubility of the Fermat relation for all but a small group of primes, and he thus laid the foundation for an eventual complete proof of Fermat’s last theorem. For his great advance, the French Academy of Sciences awarded him its Grand Prize in 1857. The ideal numbers have made possible new developments in the arithmetic of algebraic numbers. In 1861, Germany’s first seminar in pure mathematics was established at Berlin on the recommendation of Kummer and Karl Weierstrass.[9] It soon attracted gifted young mathematicians form throughout the world, including many graduate students.[3] Kummer’s Berlin lectures, always carefully prepared, covered analytic geometry, mechanics, the theory of surfaces, and number theory.
Later Life
For the rest of his life, Ernst Kummer was devoted to geometry. He applied himself with unbroken productivity to ray systems and also considered ballistic problems. By that time, also discovered the fourth order surface, now named after him, based on the singular surface of the quadratic line complex. The Kummer surface has 16 isolated conical double points and 16 singular tangent planes and was published in 1864. He retired at his own request in 1883 to spent the last years of his life in quiet retirement until his death in 1893 at age 83.
At yovisto academic video search, you can learn more about algebraic geometry in the lecture of Gregory Sankaran on Moduli of deformation generalised Kummer varieties.
Gregory Sankaran: Moduli of deformation generalised Kummer varieties, [11]
References and Further Reading:
- [1] O’Connor, John J.; Robertson, Edmund F., “Ernst Kummer“, MacTutor History of Mathematics archive, University of St Andrews.
- [2] Ernst Eduard Kummer at Encyclopedia Britannica
- [3] Kummer, Ernst Eduard, at Encyclopedia.com, Complete Dictionary of Scientific Biography
- [4] Ernst Eduard Kummer at zbMATH
- [5] Ernst Eduard Kummer at Mathematics Genealogy Project
- [6] Ernst Eduard Kummer at Wikidata
- [7] Carl Friedrich Gauss – The Prince of Mathematicians, SciHi Blog
- [8] Lejeune Dirichlet and the Mathematical Function, SciHi Blog
- [9] Karl Weierstrass – the Father of Modern Analysis, SciHi Blog
- [10] Berliner Monatsberichte (1867), 395. As translated in Robert Édouard Moritz, Memorabilia Mathematica; Or, The Philomath’s Quotation-book (1914), 185
- [11] Gregory Sankaran: Moduli of deformation generalised Kummer varieties, Hausdorff Center for Mathematics @ youtube
- [12] Timeline for Ernst Eduard Kummer via Wikidata