
Nathan Rosen (1909-1995), photo: http://www.technion.ac.il/~peres/Rosen.jpg
On March 22, 1909, US-American physicist Nathan Rosen was born. He is best known for his cooperation together with Albert Einstein and Boris Podolsky on the quantum-mechanical description of physical reality leading the the so-called Einstein-Podolsky-Rosen paradoxon, as well as his postulation of worm holes connecting distant areas in space. Although purely theoretic, his work also had an important impact on science fiction literature.
Early Years
Nathan Rosen was born in New York City. He first studied electrical engineering (bachelor’s degree) and then physics (master’s degree 1929) at the Massachusetts Institute of Technology, where he received his doctorate in 1932 with the thesis “Calculation of Energies of Diatomic Molecules” under John C. Slater. During his time at the University, Rosen already published several papers on the explanation of an atomic nucleus‘ structure and on wave functions. He then became a National Research Fellow at the University of Michigan and Princeton University, where he studied theoretical molecular physics (model of the hydrogen molecule). However, he already wrote his master’s thesis on gravitational physics and contacted Albert Einstein at Princeton to get his opinion.
The Assistant of Einstein
Rosen started his assistance job to Albert Einstein in 1935, extending Einstein’s studies on wave functions, resulting in a publication together with Boris Podolsky. In the paper, the three scientists attempted to answer the question “Can quantum-mechanical description of physical reality be considered complete?“. The effects were then named the Einstein-Podolsky-Rosen paradox (EPR). The EPR paradox contains a thought experiment, attempting to reveal insufficiencies of quantum mechanics and indeed they at least proved the research on quantum mechanics at this state was incomplete.

Artist impression of a Schwarzschild wormhole, image: Alain r, [CC BY-SA 3.0], via WikiCommons
The Einstein-Podolsky-Rosen Paradoxon
“Due to the lucidity and apparently incontestable character of the argument, the paper of Einstein, Podolsky and Rosen created a stir among physicists and has played a large role in general philosophical discussion. Certainly the issue is of a very subtle character and suited to emphasize how far, in quantum theory, we are beyond the reach of pictorial visualization.”
– Niels Bohr, (1949) as quoted in [14]
The essence of the paradox is that particles can interact in such a way that it is possible to measure both their position and their momentum more accurately than Heisenberg’s uncertainty principle allows [11], unless measuring one particle instantaneously affects the other to prevent this accuracy, which would involve information being transmitted faster than light as forbidden by the theory of relativity (“spooky action at a distance”). This consequence had not previously been noticed and seemed unreasonable at the time; the phenomenon involved is now known as quantum entanglement. According to quantum mechanics, under some conditions, a pair of quantum systems may be described by a single wave function, which encodes the probabilities of the outcomes of experiments that may be performed on the two systems, whether jointly or individually. The routine explanation of this effect was, at that time, provided by Heisenberg’s uncertainty principle. Physical quantities come in pairs called conjugate quantities. Examples of such conjugate pairs are (position, momentum), (time, energy), and (angular position, angular momentum). When one quantity was measured, and became determined, the conjugated quantity became indeterminate. Heisenberg explained this uncertainty as due to the quantization of the disturbance from measurement.
Einstein-Rosen Bridges
After working for Einstein, Rosen was suggested to continue his work in Israel. Both scientists began focusing on wormholes after discovering a mathematical method for wormholes able to connect certain areas in space. These Einstein-Rosen bridges were found by mating the mathematical solutions of black holes and white holes through using Einstein’s field equations from 1915. The Einstein-Rosen bridges, also called Schwarzschild wormholes were completely theoretical, but John A. Wheeler and Robert W. Fuller proved these wormholes in 1962 to be unstable. A wormhole can be visualized as a tunnel with two ends, each at separate points in spacetime (i.e., different locations and/or different points of time), or by a transcendental bijection of the spacetime continuum. Wormholes are consistent with the general theory of relativity, but whether wormholes actually exist remains to be seen. A wormhole could connect extremely long distances such as a billion light years or more, short distances such as a few meters, different universes, or different points in time.
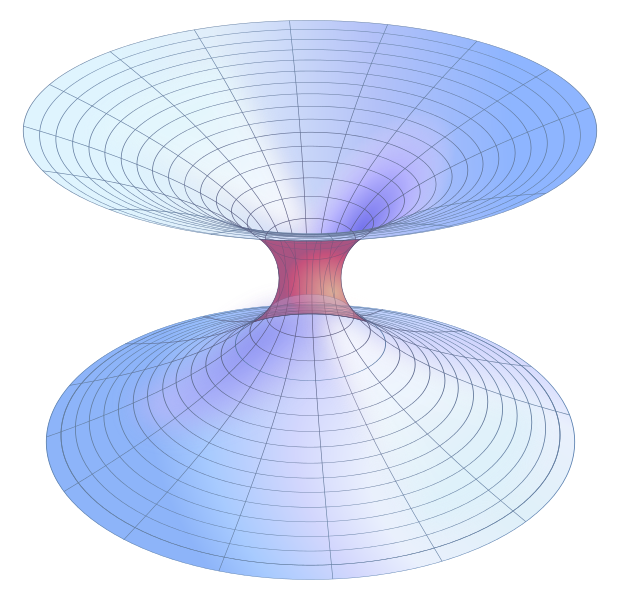
“Embedding diagram” of a Schwarzschild wormhole, image: AllenMcC. Vector: KES47, [CC BY-SA 3.0], via WikiCommons
Wormholes
According to general relativity, the gravitational collapse of a sufficiently compact mass forms a singular Schwarzschild black hole. In the Einstein–Cartan–Sciama–Kibble theory of gravity, however, it forms a regular Einstein–Rosen bridge. This theory extends general relativity by removing a constraint of the symmetry of the affine connection and regarding its antisymmetric part, the torsion tensor, as a dynamical variable. Torsion naturally accounts for the quantum-mechanical, intrinsic angular momentum (spin) of matter. The minimal coupling between torsion and Dirac spinors generates a repulsive spin–spin interaction that is significant in fermionic matter at extremely high densities. Such an interaction prevents the formation of a gravitational singularity. Instead, the collapsing matter reaches an enormous but finite density and rebounds, forming the other side of the bridge.
Wormholes in Science Fiction
However, wormholes not only fascinated scientists, also science fiction writers increased their interest in them. Numerous writers in literature, television and films used and still use wormholes to transport whole star ships or travel through time as in Star Trek’s movie from 2009 in which Spock [10] and Nero use (fictional) red matter to build artificial black holes and travel back in time. Contrary to physics, there are no limits in science fiction and even in Star Trek, a completely stable wormhole near the planet Bajor can be found, unique also in the Star Trek universe. A notable science fiction novel is also ‘The Forever War‘ by Joe Haldeman from 1974. In the plot, interstellar travel is possible through collapsars, another word for black holes. The plot is leaned on the theory by Einstein and Rosen, claiming that there may be bridges located in the black holes.
Rosen’s Later Life
Rosen later was professor of theoretical physics at the University of Kiev (on Einstein’s recommendation) and from 1941 at the University of North Carolina at Chapel Hill before going to Israel, where he was professor at the Technion in Haifa from 1953 and founder of the Institute of Theoretical Physics there. He was temporarily head of the Physics Department and the Faculty of Nuclear Engineering there. In 1977 he became Distinguished Professor at the Technion. He was emeritus in 1979, but continued to teach gravitational physics at the Technion (as Gerard Swope Professor Emeritus) until 1991. In Israel, he was also involved in building the engineering education at Ben Gurion University in Be’er Scheva (1969-1971 he was Dean of Engineering there).
Nathan Rosen died on December 18, 1995 in Haifa.
A take on time travel paradoxes | Paul Bunnell | TEDxEmbryRiddlePrescott, [15]
References and Further Reading:
- [1] Nathan Rosen at New York Times Online
- [2] Nathan Rosen Biography
- [3] Wormholes at NASA’s Website
- [4] Albert Einstein revolutionized Physics, SciHi Blog, March 14, 2018
- [5] James Chadwick and the Discovery of the Neutron, SciHi Blog, February 27, 2018
- [6] Sir Arthur Eddington – The Man who Proved Einstein’s General Relativity, SciHi Blog, November 22, 2012
- [7] The Annus Mirabilis in Physics – Albert Einstein and the Year 1905, SciHi Blog, June 30, 2012
- [8] Albert Abraham Michelson and the Famous Experiment that lead to Einstein’s Special Relativity Theory, SciHi Blog, December 19, 2012
- [9] Nathan Rosen at Wikidata
- [10] A life is like a garden – Leonard Nimoy, SciHi Blog, February 28, 2015.
- [11] Werner Heisenberg and the Uncertainty Principle, SciHi Blog, December 5, 2012.
- [12] Nathan Rosen at the Mathematics Genealogy Project
- [13] A. Einstein and N. Rosen, The Particle Problem in the General Theory of Relativity, Phys. Rev. 48, 73–77 (1935)
- [14] “Discussion with Einstein on Epistemological Problems in Atomic Physics”, in Albert Einstein: Philosopher-Scientist (1949)
- [15] A take on time travel paradoxes | Paul Bunnell | TEDxEmbryRiddlePrescott, TEDx Talks @ youtube
- [16] Timeline of Quantum Physics People, via DBpedia and Wikidata





