
Goethe’s symmetric colour wheel with associated symbolic qualities, watercolor pen and ink drawing by Goethe, 1809, original: Freies Deutsches Hochstift – Frankfurt Goethe Museum
On August 28, 1749, famous German writer and statesman Johann Wolfgang von Goethe was born. Besides his merits in literature, poetry, and philosophy, that we already did acknowledge in previous articles [4,5,9], Goethe was also interested in natural sciences. He independently discovered the human intermaxillary bone in 1784, was one of the many precursors in the history of evolutionary thought, popularized the Goethe barometer using a principle established by Torricelli, and published his Theory of Colours in 1810, which he considered his most important work. In his Farbenlehre (Theory of Colours), Goethe was vehemently opposed to Newton’s analytic treatment of color, but nevertheless his theory failed.[8]
Goethe’s Theory of Colours
By the time Johann Wolfgang von Goethe developed his interest in natural sciences, Isaac Newton’s color theory was already generally acknowledged. However, as Goethe later wrote
“… as I looked at a white wall through the prism, that it stayed white! That only where it came upon some darkened area, it showed some colour, then at last, around the window sill all the colours shone… It didn’t take long before I knew here was something significant about colour to be brought forth, and I spoke as through an instinct out loud, that the Newtonian teachings were false.” [7]
With this starting point, Goethe developed his “theory” while at the same time refraining from setting up a theory, as he put it “its intention is to portray rather than explain“. Goethe proceeded to develop a wide range of interrogations through which he would reveal the essential character of color. As it was later explained by David Seamon, “the crux of [Goethe’s] color theory is its experiential source: rather than impose theoretical statements, Goethe sought to allow light and color to be displayed in an ordered series of experiments that readers could experience for themselves“. In his essay ‘The experiment as mediator between subject and object‘ from 1772, Goethe outlined his method and put an emphasis on his standpoint:
“The human being himself, to the extent that he makes sound use of his senses, is the most exact physical apparatus that can exist.”
Light spectrum, from Theory of Colours. Goethe observed that with a prism, colour arises at light-dark edges, and the spectrum occurs where these coloured edges overlap.
Experiments and Observations
In concerns of light and dark, Goethe understood darkness as polar to and interacting with light and color as the result of the interaction of light and shadow. Goethe performed experiments which examined the effects of turbid media like air, dust and moisture on the perception of light and dark. He made the observation that light seen through a turbid medium appears yellow, and darkness seen through an illuminated medium appears blue.
Violet is unnecessary
Johann Wolfgang von Goethe also proposed a symmetric color wheel and put emphasis on the importance of magenta, in contrast to Newton, who counted only spectral colors as fundamental. In his color wheel, Goethe also included several aesthetic qualities titled as “allegorical, symbolic, mystic use of colour“. Goethe apparently associated red with ‘beautiful’, green with ‘useful’, violet with ‘unnecessary’ and blue with ‘common’.
Reception
The first edition of Zur Farbenlehre was published in an edition of 500 copies on white paper and 250 copies on gray paper by Cotta’sche Verlagsbuchhandlung. It contained three sections: a didactic section in which Goethe presents his own observations, a section in which he makes his case against Newton, and a historical section. In the same year, the mathematician, physicist, and astronomer Carl Brandan Mollweide refuted Goethe’s view of the origin of colors in the paper Prüfung der Farbenlehre des Herrn v. Goethe und Vertheidigung des Newton’schen Systems wider dieselbe (Examination of Mr. v. Goethe’s Theory of Colors and Defense of Newton’s System Against It), which was published in Halle (Saale). When it was translated by Charles Eastlake into English in 1840, he left out the part were Goethe made his case against Newton. Goethe’s experiments probe the complexities of human colour perception. While Newton sought to develop a mathematical model for the behaviour of light, Goethe focused on exploring how colour is perceived in a wide array of conditions. Edwin Land’s retinex theory from 1971 show many similarities to Goethe’s theory. Unlike Newton, Goethe’s concern was not so much with the analytic treatment of colour, as with the qualities of how phenomena are perceived. Philosophers have come to understand the distinction between the optical spectrum, as observed by Newton, and the phenomenon of human colour perception as presented by Goethe — a subject analyzed at length by Wittgenstein in his comments on Goethe’s theory in Remarks on Colour.
Goethe’s Self Assessment
Goethe himself valued the results of his research on color more highly than his entire literary output. Even in his old age, he said to his secretary Johann Peter Eckermann:
“I do not imagine anything about everything I have achieved as a poet. […] But the fact that I am the only one in my century who knows what is right in the difficult science of color theory is something I take credit for.”
Pehr Sällström, On the compatibility of Goethe’s colour theory with that of Newton | colour.education [13]
References and Further Reading:
- [1] Goethe’s Theory of Color
- [2] Exploratory experimentation: Goethe, land, and color theory
- [3] Theory of Colours at MIT
- [4] The Life and Works of Johann Wolfgang von Goethe, SciHi Blog
- [5] Goethe’s Muse Charlotte von Stein, SciHi Blog
- [6] Goethe Got Married, SciHi Blog
- [7] Goethe, Goethes Werke, Weimar: Hermann Böhlau, 1887–1919, II. Abtheilung: Naturwissenschaftliche Schriften, Bd. 4, pp. 295–296
- [8] Standing on the Shoulders of Giants – Sir Isaac Newton, SciHi Blog
- [9] Goethe’s Most Famous Poem – Wanderers Nachtlied, SciHi Blog
- [10] John Tyndall, “Goethe’s Farbenlehre-(Theory of Colors) I“, in Popular Science Monthly, Vol. 17, June 1880.
- [11] John Tyndall, “Goethe’s Farbenlehre-(Theory of Colors) II“, in Popular Science Monthly, Vol. 17, July 1880.
- [12] Duck, Michael J (1988). “Newton and Goethe on colour: Physical and physiological considerations”. Annals of Science. 45 (5): 507–519
- [13] Pehr Sällström, On the compatibility of Goethe’s colour theory with that of Newton, at Philosophicum Basel, colour.education @ youtube
- [14] Johann Wolfgang von Goethe at Wikidata
- [15] Timeline for Johann Wolfgang von Goethe, via Wikidata






Thanks Tabea, for a well written introduction outlining a brief context in history of Goethe’s work on Colour as well as its general place within the natural sciences. Your article receives the TheoryOfColor.org stamp of approval!
Isaac Newton’s Scam Spectrum – Several ways to make it observable and how they disprove his colour theory
R.S.W.Bobbette 2018
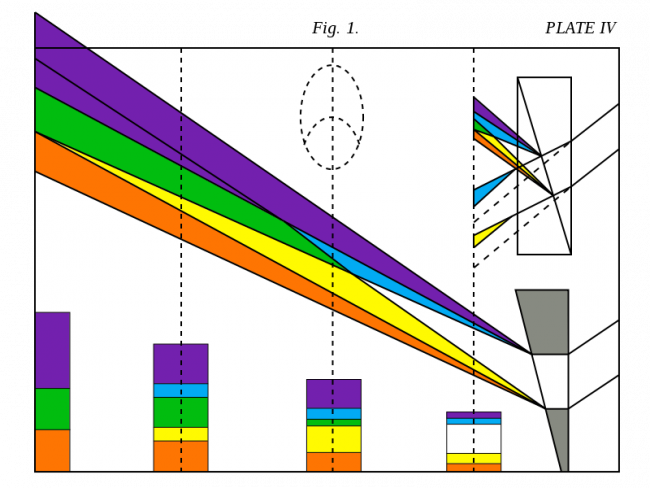
The repeatedly observable fact is that colours generated in and through prisms never originate from a “rainbow spectrum”, but always from pairs of variably separated bands of colours related to relative dark-light contrasts. These bands are about equal in overall width, with the central stripe of each less distinct than the outer two. Initially, no green colour occurs nor any spectrum. The appearance of a “rainbow spectrum” is a secondary effect, a parlour trick that can be accomplished in several instructive ways.
The first method is the one used by Newton to put over his farcical, but mathematically accessible, idea of colour production. Of course, the method of the scam in this case is to reduce the body of white light to where the otherwise and actually separate colour bands slightly overlap or intersect to produce green. This is the basic principle of all forms of the scam. This first method allows a portable result, the narrow beam of light, to avoid the embarrassing drawing together of the two pre-existing colour bands, where the colours actually originate. The fact that the colour bands arise separated by variable distances (i.e. refractive angles) means that the blue colour is not the “other half” of the same light that is behind the red band. This is only implied by the scam spectrum. The scam spectrum also hides, or makes hard to discriminate, that the purple and violet stripes of the blue colour band are actually projected or illuminated in front of relative darkness, from the side; the complete red colour band is clearly seen to be shone through from behind. These three facts do not readily suggest a uniform approach along any lines put forward by Newton, etc. The “rainbow spectrum” is not created by one unified beam of light being split into colours, but from two diametrically opposite, separate beams of already coloured light being brought together by reducing what separates them to where they combine to create the otherwise non-existent green colour. An equally applied “differential refraction” is not an option.
This first example has the light going through the prism and the colours being observed on a surface. It is also possible to create the scam by observing the colour bands directly through the prism. If you look at a bright window, through a prism, you will notice the colour bands on either side of the window, along the line of refraction. Now we can see the reason for a concept like refraction, when we twist the prism back and forth and see the dramatic narrowing and broadening of the light image of the window. This measurable phenomenon is the basis of refraction, and therefore of differential refraction, and it is this that allows us to produce a second version of Newton’s Scam Spectrum. If you twist the prism far enough, you reduce the light of the window to where – voila! – you have the “rainbow spectrum”, down the line of refraction.
But there are some problems here. No matter how you broaden or shrink the window image, the colour bands remain unaltered to any visible extent. This at least suggests that they occur after the light is bent. They merely move and follow the light-dark contrast line. When brought together, both bands move towards the narrow angle of the prism, but the red one moves much more quickly and “catches up” with the blue. They remain unaltered until reaching the scam spectrum, when they begin to overlap or intersect, with the yellow and blue stripes changing to green, until they merge and are replaced by one green stripe. Only now do the colour bands begin to shrink, but not equally. Orange and purple disappear first, with red, green and violet disappearing together as the light is choked off.
Furthermore, the colour bands have the ability to move in two different directions, or at different speeds, within themselves. Let me explain. There is a small shelf edge projecting into the window view, and this shows the identical red band as the side of the window, but much shorter and projected about one and a half band widths into the window. Now as you tilt the prism to shrink the window, this shelf projection shrinks in accord with refraction, until about three colour band widths from the blue band, it disappears into the overall edge. But throughout this entire span, the small colour band has been following the shrinking shelf, moving backwards into the main edge colour band while the whole moves forward. No “differential refraction” can accommodate these appearances, disappearances and movements.
Prisms certainly should be accorded much more honest, interested study. Another way of producing Newton’s Scam Spectrum requires a bit of set-up but is, I think, worth the interesting results.
Take flat black and flat white paint, mix equally to paint grey a pole 2 inches wide and 5 feet high. Paint a piece of cardboard 2×5 feet flat black and a piece 2×3 feet flat white (it’s relative dimensions and not actual measurements that matter). Stand the grey pole in front of the black board in bright light, and look at it through the prism. You will see the clearest “rainbow spectrum” down the line of the pole. There are two ways of showing this to be a version of Newton’s Scam Spectrum. To do the first you put the white board over the lower half of the black, and look; suddenly at the white border the blue band turns to red and the red to blue, continuing down the line of refraction. So we have the remarkable anachronism of Newton’s Scam Spectrum cheek to jowl with a “complete” inverted spectrum, with red meeting violet in the middle! Placing the white just to the right or the left of the pole produces a “complete spectrum” of either two red or two blue bands…
The creation of colour in a prism is repeatedly seen to be more closely related to relative dark-light contrasts than to either refraction or any necessary red – blue continuum. This change of colour from blue to red down the line of refraction, merely because the background changes from relatively dark to relatively light, shows up as lies all the concepts of prismatic colour production put forward by Newton and his idolizers. The fact that the blue band abuts the red one on the same line of refraction is also absolute proof that, far from being parts of a rightfully belonging together “rainbow spectrum”, the colour bands are indirectly related to each other at best. This shows the absurdity (if previous evidence hasn’t) of there being any possibility of refraction, differential or otherwise, in the production of these phenomena of colour. The only certain relationship to refraction is the left-right orientation of the bands, and probably their width.
The trick to Newton’s Scam Spectrum in this case is the narrowness of the pole. Staple a sheet of writing paper to the pole and you will see the colour bands separated.
Finally, and less explicitly, by twisting around a prism in sizeable bright light, the “rainbow spectrum” can be seen projected onto surfaces, represented by at least three examples. One duplicates the window method, with a bright spot that is reduced by twisting the prism until the bands meet. Another has the bright spot visible on a card near the prism, but reducing in size until 8-10 feet away (in this example) a “spectrum” appears. The third traces back to the ninety degree angles of the prism, but shows no bright spot. It is aligned with the bands on either side of the angle and is certainly a projective version of the narrow pole effect.
These are the few methods I have been able to attempt; I’m sure there are others. Again, every supposed colour spectrum arising from a prism can be resolved into the actually existing separate colour bands. These arise in prisms at opposite sides of the body of light, adjacent to relative darkness. The light involved in the red side of the scam spectrum is not involved in the creation of the blue side.
PostScript…
It should be noted that the “inverted spectrum” compresses to produce a magenta stripe that replaces the red and violet ones, as the otherwise non-existent green replaces the blue and yellow. Any physics of prismatic colour relationships, that is not fantasy, will have to address four initially occurring colours, plus four derived from their combining. The prismatic “seven colours of the rainbow spectrum”, with everything derived from it, have been made up for mathematical convenience and easy salesmanship, and do not represent soundly reported investigative science.