
Georg Friedrich Bernhard Riemann (1826-1866)
On September 17, 1826, influential German mathematician Bernhard Riemann was born. Riemann‘s profound and novel approaches to the study of geometry laid the mathematical foundation for Albert Einstein’s theory of relativity. He also made important contributions to the theory of functions, complex analysis, and number theory.
“Nevertheless, it remains conceivable that the measure relations of space in the infinitely small are not in accordance with the assumptions of our geometry [Euclidean geometry], and, in fact, we should have to assume that they are not if, by doing so, we should ever be enabled to explain phenomena in a more simple way.”
– Bernhard Riemann, Memoir (1854)
Bernhard Riemann – Early Years
Bernhard Riemann was born in Breselenz, a village near Dannenberg in the Kingdom of Hannover, today in Germany, as the second of six children to Friedrich Bernhard Riemann, a poor Lutheran pastor who had fought in the Napoleonic Wars. Friedrich Riemann acted as teacher to his children and he taught Bernhard until he was ten years old. Bernhard Riemann exhibited exceptional mathematical skills, such as calculation abilities, from an early age but suffered from timidity and a fear of speaking in public.
In 1840 Bernhard entered directly into the third class at the Lyceum in Hannover, living with his grandmother but, in 1842, his grandmother died and Bernhard moved to the Johanneum Gymnasium in Lüneburg. He showed a particular interest in mathematics and the school director allowed Bernhard to study mathematics texts from his own library. On one occasion he lent Bernhard Legendre’s book on the theory of numbers and Bernhard read the 900 page book in six days.[1] In 1846, at the age of 19, he started studying philology and theology at the University of Göttingen in order to become a pastor and help with his family’s finances. However, once there, he began studying mathematics under Carl Friedrich Gauss, who recommended that Riemann give up his theological work and enter the mathematical field.[3]
From Göttingen to Berlin
Riemann moved from Göttingen to Berlin University in the spring of 1847 to study under Jakob Steiner, Carl Gustav Jakob Jacobi, Peter Gustav Lejeune Dirichlet and Gotthold Eisenstein.[4] It was during his time at the University of Berlin that Riemann worked out his general theory of complex variables that formed the basis of some of his most important work.
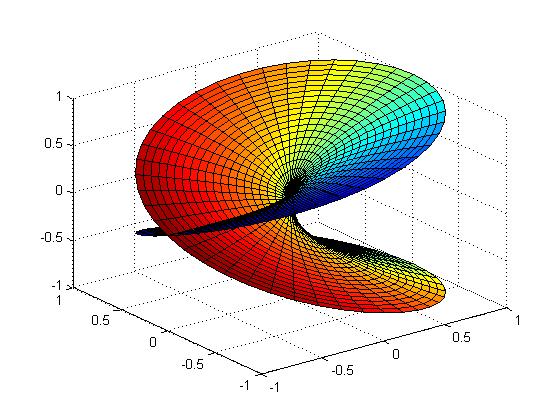
A riemann surface for the complex function f(z) = sqrt(z)
Riemann Surfaces and Research in Topology
In 1849 he returned to Göttingen and his Ph.D. thesis, supervised by Gauss, was submitted in 1851. Riemann’s thesis studied the theory of complex variables and, in particular, what we now call Riemann surfaces. It therefore introduced topological methods into complex function theory. In 1851 and in his more widely available paper of 1857, Riemann showed how such surfaces can be classified by a number, later called the genus, that is determined by the maximal number of closed curves that can be drawn on the surface without splitting it into separate pieces. This is one of the first significant uses of topology in mathematics.[2] The work builds on Cauchy’s foundations of the theory of complex variables built up over many years. In proving some of the results in his thesis Riemann used a variational principle which he was later to call the Dirichlet Principle since he had learnt it from Dirichlet’s lectures in Berlin.[1]
Riemannian Geometry
On Gauss’s recommendation Riemann was appointed to a post in Göttingen and he worked for his Habilitation on the foundations of geometry. Over many months, Riemann developed his theory of higher dimensions and delivered his lecture at Göttingen in 1854 entitled Über die Hypothesen welche der Geometrie zu Grunde liegen (“On the hypotheses which underlie geometry“), published posthumously by Dirichlet in 1868. This should be the foundation of the field of Riemannian geometry and thereby set the stage for Einstein’s general theory of relativity.[5] Riemann found the correct way to extend into n dimensions the differential geometry of surfaces. The fundamental object is called the Riemann curvature tensor. For the surface case, this can be reduced to a number (scalar), positive, negative or zero; the non-zero and constant cases being models of the known non-Euclidean geometries. Riemann’s idea was to introduce a collection of numbers at every point in space (i.e., a tensor) which would describe how much it was bent or curved. Riemann found that in four spatial dimensions, one needs a collection of ten numbers at each point to describe the properties of a manifold, no matter how distorted it is. This is the famous construction central to his geometry, known now as a Riemannian metric.
Riemann Hypothesis
In 1857, there was an attempt to promote Riemann to extraordinary professor status at the University of Göttingen. Although this attempt failed, it did result in Riemann finally being granted a regular salary. In 1859, following Lejeune Dirichlet’s death, he was promoted to head the mathematics department at Göttingen. In the same year he was elected a corresponding member of the Berlin Academy of Sciences. Also in 1859 Riemann introduced complex function theory into number theory. He took the zeta function, which had been studied by many previous mathematicians because of its connection to the prime numbers, and showed how to think of it as a complex function.[2] About his eponymous zeta function, which is important for understanding the distribution of prime numbers, he stated the famous (and still not completely proven) Riemann hypothesis, a conjecture that the non-trivial zeros of the Riemann zeta function all have real part 1/2.
Riemann’s Influence
Riemann’s influence was initially less than it might have been. Göttingen was a small university, Riemann was a poor lecturer, and, to make matters worse, several of his best students died young. His few papers are also difficult to read, but his work won the respect of some of the best mathematicians in Germany.[2]
Physicists were still far removed from such a way of thinking: space was still, for them, a rigid, homogeneous something, susceptible of no change or conditions. Only the genius of Riemann, solitary and uncomprehended, had already won its way by the middle of the last century to a new conception of space, in which space was deprived of its rigidity, and in which its power to take part in physical events was recognized as possible. (Albert Einstein)
However, in 1862, shortly after his marriage to Elise Koch, Riemann fell seriously ill with tuberculosis. Repeated trips to Italy failed to stem the progress of the disease. Riemann fled Göttingen when the armies of Hanover and Prussia clashed there in 1866. He died during his journey to Italy in the same year.
Barry Mazur, A Lecture on Primes and the Riemann Hypothesis, [8]
References and Further Reading:
- [1] O’Connor, John J.; Robertson, Edmund F., “Bernhard Riemann“, MacTutor History of Mathematics archive, University of St Andrews.
- [2] Bernhard Riemann at Britannica Online
- [3] Carl Friedrich Gauss – The Prince of Mathematicians, SciHi blog, April 30, 2013.
- [4] Lejeune Dirichlet and the Mathematical Function, SciHi blog, Feb 13, 2015.
- [5] Albert Einstein revolutionized Physics, SciHi blog, Mar 14, 2013.
- [6] Bernhard Riemann at zbMATH
- [7] Bernhard Riemann at Wikidata
- [8] Barry Mazur, A Lecture on Primes and the Riemann Hypothesis, Harvard University, Gratuate Mathematics @ youtube
- [9] The Mathematical Papers of Georg Friedrich Bernhard Riemann
- [10] Monastyrsky, Michael (1999), Riemann, Topology and Physics, Boston, MA: Birkhäuser.
- [11] Ji, Lizhen; Papadopoulos, Athanese; Yamada, Sumio, eds. (2017). From Riemann to Differential Geometry and Relativity. Springer.
- [12] Timeline of Bernhard Riemann via Wikidata





