
Wacław Sierpiński ( 1882 – 1969)
On March 14, 1882, Polish mathematician Wacław Franciszek Sierpiński was born. Sierpiński is known for contributions to set theory, research on the axiom of choice and the continuum hypothesis, number theory, theory of functions and topology. Three well-known fractals are named after him (the Sierpiński triangle, the Sierpiński carpet and the Sierpiński curve), as are Sierpiński numbers and the associated Sierpiński problem.
Wacław Sierpiński – Early Years in Russian occupied Poland
Wacław Franciszek Sierpiński was born in Warsaw, at the time part of the Russian Empire, today Poland, the son of Konstanty Sierpiński, a doctor, and his mother Ludwika, née Łapińska. Sierpiński’s exceptional talent for mathematics was discovered while he was still in elementary school. However, education was difficult during the period of Russian rule over Poland. Nevertheless, in 1900, at the age of eighteen, Sierpiński finished the fifth gymnasium in Warsaw – Warsaw had belonged to Russia since the Third Partition of Poland in 1795 – and from 1899 studied mathematics and physics at the tsarist University of Warsaw. The lectures were all given in Russian. In 1903 there was a competition in the mathematics department of the university on Voronoy‘s number theory. Sierpiński wrote his first scientific paper on this and won the gold medal.
The journal Izvestia of Warsaw University wanted to publish this work, but Sierpiński refused to publish it in Russian. Thus, the work was not published until four years later, in 1907, in a Polish-language mathematical journal. All students had to attend Russian classes during their studies and take an exam. It was considered a matter of honor among Polish patriots to do as poorly as possible on this exam. Sierpiński did not answer a single question in the test and received the grade Poor. He turned down the offer of a retake. Fortunately, a professor had mercy on him and gave him a “Good” in Russian. Thus, Sierpiński was able to finish his studies in 1904 at the age of 22.
Graduation and first Textbooks
In the fall of the same year, he taught mathematics and physics at a girls’ high school. Because of a strike against Russification, this school was closed and Sierpiński moved to Kraków, which belonged to Austria-Hungary, to study philosophy and astronomy in addition to mathematics. In 1906 he was awarded a doctorate in philosophy. In 1907 he spent a few months in Göttingen to work with the Polish mathematician Tadeusz Banachiewicz. In July 1908, at the age of 26, he habilitated at the University of Lviv and taught there until 1914. In the period from 1910 to 1914, his first books Theory of Irrational Numbers, Outline of Set Theory, and The Theory of Numbers were published.
Russian Years
At the outbreak of World War I in 1914, he fled with his family to Belarus to his parents-in-law’s estate. As a supposed Austrian, he was interned in Vyatka (renamed Kirov in 1934). Moscow mathematician friends managed to bring him to the Russian capital in 1915, where he remained until the end of the war. During this time he collaborated with the Russian mathematician Nikolai Nikolaevich Luzin. In 1918, he returned to Poland via Finland and Sweden, where he taught first in Lviv and then at Warsaw University, and remained until the end of his life. He founded the important journal Fundamenta Mathematicae together with other representatives of the so-called Warsaw School of Mathematics. Sierpiński edited the journal, which specialized in papers on set theory.
During the Polish-Soviet War in 1920, he worked at Biuro Szyfrów, the “cipher bureau” of the General Staff, on deciphering Soviet secret codes. In the interwar period he led a busy scientific life and worked a lot on set theory. He published eight new books, two pamphlets, and seven textbooks. Sierpiński was a member of many scholars’ associations in and outside Poland. He represented his country at mathematical congresses. In 1932 he gave a plenary lecture at the International Congress of Mathematicians in Zurich (Sur les ensembles de points qu’on sait définir effectivement, On the sets of points that we know how to effectively define).
![Sierpinski "square curve"[2] of orders 2-4](http://scihi.org/wp-content/uploads/2021/03/Sierpinski_curve_orders_2-4-650x217.png)
Sierpinski “square curve” of orders 2-4
During this period, Sierpiński worked predominantly on set theory, but also on point set topology and functions of a real variable. In set theory he made contributions on the axiom of choice and on the continuum hypothesis. In mathematics, the axiom of choice, or AC, is an axiom of set theory equivalent to the statement that a Cartesian product of a collection of non-empty sets is non-empty. Informally put, the axiom of choice says that given any collection of bins, each containing at least one object, it is possible to make a selection of exactly one object from each bin, even if the collection is infinite. The axiom of choice was formulated in 1904 by Ernst Zermelo in order to formalize his proof of the well-ordering theorem. The continuum hypothesis a hypothesis about the possible sizes of infinite sets. In particular, it states that there is no set whose cardinality is strictly between that of the integers and the real numbers. Sierpiński also proved that Zermelo–Fraenkel set theory together with the Generalized continuum hypothesis imply the Axiom of choice.
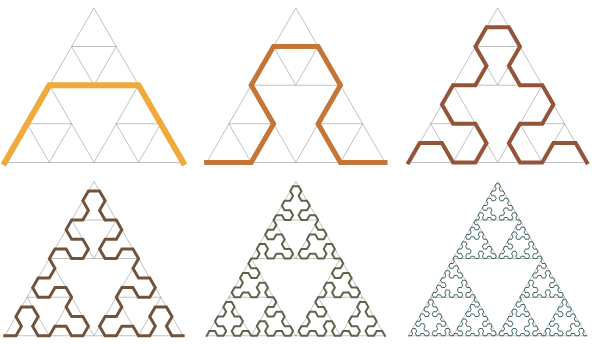
Evolution of Sierpiński arrowhead curve
He also worked on what is now known as the Sierpiński curve. The Sierpiński curves are a recursively defined sequence of continuous closed fractal curves. The Sierpiński curve is an example of a space-filling curve. Sierpiński continued to collaborate with Luzin on investigations of analytic and projective sets. His work on functions of a real variable includes results on functional series, differentiability of functions and Baire’s classification.
World War II
During World War II, he remained in Warsaw, where he formally worked for the Warsaw Municipality during the German occupation, but actually taught at the Polish Underground University. Sierpiński managed to smuggle his papers to Italy, where they were published. Under each of his papers was written: the proofs of these theories will be published in the Fundamenta Mathematicae publications. Everyone understood that it was supposed to mean that Poland would survive. After the suppression of the Warsaw Uprising in October 1944, the German troops systematically destroyed the city. The Sierpińskis’ apartment also went up in flames, the precious library was lost; likewise, the university library burned down, the private libraries of three other Warsaw mathematics professors were destroyed, and with them almost all of the 32 volumes of Fundamenta Mathematicae. More than half of all the lecturers of the mathematics department of the university perished. These losses spurred Sierpiński to produce new writings and books. He was prolific throughout his life, authoring a total of the astonishing number of 724 articles and 50 books.
Later Years
Via the camp in Pruszków outside Warsaw, he arrived in Kraków in February 1945. After a semester at the Jagiellonian University, he returned to his chair in the fall and again edited the journal Fundamenta Mathematicae. In 1946 he was awarded the Stefan Banach Prize. From 1948 he worked at the State Mathematical Institute, and after it became part of the Polish Academy of Sciences, he was head of the Science Council from 1953 to 1967. From 1956 to 1969 he was editor of the journal Acta Arithmetica, which had also been published before the war. In 1948 he became a corresponding member of the Académie des sciences, and in 1960 he became a foreign member (associé étranger). In 1960 he retired, but held a seminar on number theory at the Polish Academy of Sciences until 1967. In 1964 he was one of the signatories of the so-called Letter of 34 to Prime Minister Józef Cyrankiewicz regarding freedom of culture. He was Invited Speaker at the ICMs in Toronto in 1924, in Bologna in 1928, in Zurich in 1932, and in Oslo in 1936. Sierpiński died in Warsaw on October 21, 1969, at the age of 87.
Fractals: The Geometry of Chaos – Christmas Lectures with Ian Stewart, [5]
References and Further Reading:
- [1] John J. O’Connor, Edmund F. Robertson: Waclaw Sierpinski. In: MacTutor History of Mathematics archive.
- [2] Mathematics Genealogy Project: Wacław Sierpiński
- [3] K. Kuratowski. “Wacław Sierpiński (1882-1969)” . Acta Arithmetica. 21: 1–5.
- [4] Sierpiński: Fractals, Code Breaking, and a Crater on the Moon
- [5] Fractals: The Geometry of Chaos – Christmas Lectures with Ian Stewart, The Royal Institution @ youtube
- [6] Weisstein, Eric W. “Sierpiński Curve”. MathWorld.
- [7] Wacław Franciszek Sierpiński at zbMATH
- [8] Wacław Franciszek Sierpiński at German National Library
- [9] Wacław Franciszek Sierpiński at Wikidata
- [10] Wacław Sierpiński at the Mathematics Genealogy Project
- [11] A. Schinzel. “Wacław Sierpinski’s papers on the theory of numbers”. Acta Arithmetica. 21: 7–13.
- [12] Timeline for Wacław Franciszek Sierpiński, via Wikidata





