
Roy Kerr with his wife, photo: Melirius, CC BY-SA 3.0, via Wikimedia Commons
On May 16, 1934, New Zealand mathematician Roy Kerr was born. Kerr is best known for discovering the Kerr geometry, an exact solution to the Einstein field equation of general relativity. His solution models the gravitational field outside an uncharged rotating massive object, including a rotating black hole.
Roy Kerr – Early Years
Roy Kerr was educated at the private school St Andrew’s College. His talent for mathematics was first recognized during his highschool years. Although there was no maths teacher there at the time he was able in 1951 to go straight into third year Mathematics at the Canterbury University College of the University of New Zealand. Unfortunately, the regulations regulations did not permit him to graduate until 1954 and so it was not until September 1955 that he moved to the University of Cambridge, where he earned his PhD in 1959. His dissertation concerned the difficult problem of the equations of motion in general relativity.
The Kerr Vacuum Solution
After shortly working as a post-doctoral student at Syracuse University, Kerr began working for the United States Air Force at Wright-Patterson Air Force Base. In the 1960s, Kerr moved to the University of Texas at Austin. There, he discovered the Kerr vacuum solution. Starting from 1971, Kerr returned to the University of Canterbury in New Zealand. Kerr remained there until his retirement from his position as Professor of Mathematics.
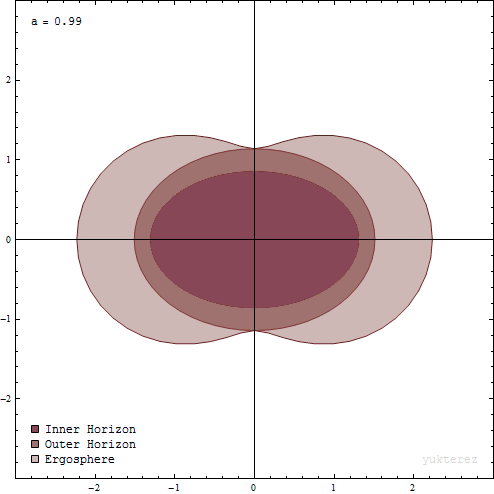
The boundaries of a Kerr black hole relevant to astrophysics. Note that there are no physical “surfaces” as such. The boundaries are mathematical surfaces, or sets of points in spacetime, relevant to analysis of the black hole’s properties and interactions, by Yukterez (Simon Tyran, Vienna), CC BY-SA 4.0, via Wikimedia Commons
The Kerr Geometry
Roy Kerr is probably best known for discovering the Kerr geometry, which is the geometry of empty spacetime around a rotating uncharged axially-symmetric black hole with a spherical event horizon. It is an exact solution of the Einstein field equations of general relativity. These kinds of equations are highly non-linear, which makes exact solutions very difficult to find. The Kerr metric is a generalization of the Schwarzschild metric, which was discovered by Karl Schwarzschild in 1915 and which describes the geometry of spacetime around an uncharged, spherically-symmetric, and non-rotating body.[4] The solution for a charged, spherical, non-rotating body, the Reissner–Nordström metric, was discovered soon afterwards in the late 1910s. However, it was Roy Kerr who managed to find the exact solution for an uncharged, rotating black-hole. The natural extension to a charged, rotating black-hole, the Kerr–Newman metric, was discovered shortly thereafter in 1965.
Honours
In 1984 Kerr received the Hughes Medal of the Royal Society in London and in 2006 the Marcel Grossmann Award. The Royal Society of New Zealand awarded him its Hector Medal in 1982 and the Rutherford Medal in 1993. At the beginning of 2011 he was admitted to the New Zealand Order of Merit for his achievements in astrophysics as a Companion (CNZM). In 2013 he received the Albert Einstein Medal,[6] in 2016 the Crafoord Prize. From 1971 until his retirement in 1993, he returned to the University of Canterbury in Christchurch (New Zealand) as Professor of Mathematics and headed the Faculty of Mathematics as Dean for ten years. Since his retirement, Kerr has lived a very secluded life.
Arne Ardeberg, Spinning Black Holes, [8]
References and Further Reading:
- [1] John J. O’Connor, Edmund F. Robertson: Roy Kerr. In: MacTutor History of Mathematics archive.
- [2] The Kerr Spacetime at Cambridge
- [3] Could A Kerr Black Hole Be Used To Travel Through Time? at Strange Dimensions
- [4] Karl Schwarzschild and the Event Horizon, SciHi Blog
- [5] Roy Kerr at Wikidata
- [6] Albert Einstein revolutionized Physics, SciHi Blog
- [7] Brian Woods: Professor Roy Kerr. In: NZMS Newsletter. No. 58, August 1993.
- [8] Arne Ardeberg, Spinning Black Holes, un 2, 2016 Crafoord Laureate 2016: Roy Kerr, University of Canterbury, Christchurch, New Zealand. Introduction by Arne Ardeberg, Lund University, Sweden. Vetenskapsakademien @ youtube
- [9] Kerr, Roy P. (1 September 1963). “Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics”. Physical Review Letters. American Physical Society (APS). 11 (5): 237–238
- [10] Kerr, R. P. & Schild, A. (1965). “Some algebraically degenerate solutions of Einstein’s gravitational field equations”. Proc. Symp. Appl. Math. 17: 119.
- [11] Timeline of Relativity Theorists, via DBpedia and Wikidata





