G. H. Hardy

G. H. Hardy and the aesthetics of Mathematics

1. December 2022 Harald Sack

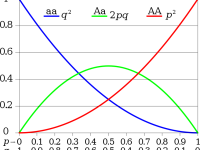
On December 1, 1947, English mathematician G. H. Hardy passed away. Hardy is known for his achievements in number theory and mathematical analysis, but also for his 1940 essay on the aesthetics of mathematics, A Mathematician’s Apology, and for mentoring the brilliant Indian mathematician Srinivasa Ramanujan. “A mathematician … has no material to work with but ideas, and so his patterns are likely to last longer, since ideas wear less with time…

computer science

Norbert Wiener and the Science of Cybernetics

26. November 2020 Harald Sack

On November 26, 1894, American mathematician Norbert Wiener was born. Wiener established the science of cybernetics, a term he coined, which is concerned with the common factors of control and communication in living organisms, automatic machines, and organizations. He attained international renown by formulating some of the most important contributions to mathematics in the 20th century. “Scientific discovery consists in the interpretation for our own convenience of a system of existence which has…

biology

Wilhelm Weinberg and the Genetic Equilibrium

13. January 2019 Tabea Tietz

On January 13, 1908, German physician and obstetrician-gynecologist Wilhelm Weinberg delivered an exposition of his ideas on the principle of genetic equilibrium in a lecture before the Verein für vaterländische Naturkunde in Württemberg. He developed the idea of genetic equilibrium independently of British mathematician G. H. Hardy.[4] Wilhelm Weinberg – Early Years Wilhelm Weinberg was born in Stuttgart, Kingdom of Württemberg (today Germany). His father Julius Weinberg, a merchant, had Jewish roots, but he…

mathematics

What’s your Erdös Number? – The bustling Life of Mathematician Paul Erdös

20. September 2018 Harald Sack

On September 20, 1996, Hungarian mathematician Paul Erdös passed away. He published more scientific papers than any other mathematician in history, with hundreds of collaborators. Thus, he even created a ‘small world’ of its own, the famous club of people that posess an ‘Erdös Number‘. BTW, my Erdös number is 3, i.e. I have published a paper together with a co-author whose Erdös number is 2. In this little game of numbers,…

mathematics

Although I Cannot Prove it… – The Famous Goldbach Conjecture

7. June 2018 Harald Sack

On the 7th of June 1742, Prussian mathematician Christian Goldbach wrote a letter to his famous colleague Leonard Euler, which should make history. Well, at least in the mathematical world. In this letter Christian Goldbach refined an already previously stated conjecture from number theory concerning primes to his friend Euler, which by today is known as the famous Goldbach conjecture. It states: Every even integer greater than 2 can be expressed as the…

mathematics

The Short Life of Srinivasa Ramanujan

22. December 2016 Harald Sack

On December 22, 1887, Indian mathematician and autodidact Srinivasa Ramanujan was born. Though he had almost no formal training in pure mathematics, he made major contributions to mathematical analysis, number theory, infinite series, and continued fractions. Supported by English mathematician G. H. Hardy from Cambridge, Ramanujan independently compiled nearly 3,900 results during his short life, which all have been proven correct. “Sir, an equation has no meaning for me unless it expresses…

biology

Sewall Wright and the Importance of Population Genetics

21. December 2016 Tabea Tietz

On December 21, 1889, American geneticist Sewall Green Wright was born. Wright is known for his influential work on evolutionary theory and also for his work on path analysis. He was a founder of population genetics alongside Ronald Fisher and J.B.S. Haldane,[4] which was a major step in the development of the modern evolutionary synthesis combining genetics with evolution. Early Years and Academic Career Sewall Wright‘s father Philip Green Wright was a…