And Kepler Has His Own Opera – Kepler’s 3rd Planetary Law

Johannes Kepler (1571-1630), portrait by an unknown artist (c. 1620)

On May 15, 1618, famous astronomer Johannes Kepler discovered the 3rd and also last of his planetary laws, and concluded the general revolution of our celestial world that started with Nicolaus Copernicus about 100 years earlier.[1] And that made him rather popular as he still is today. Did you know that there is a Kepler crater on the Moon, a Kepler crater on Mars, a Kepler asteroid, a Kepler supernova, of course there has to be a space mission named after him, even an opera (‘Die Harmonie der Welt‘ by Paul Hindemith…unfortunately not available at yovisto…at least by now), a Kepler mountain, various universities (including the Johannes Kepler University at Linz in Austria), a Kepler building and even a Kepler graphic processing unit (GPU) on a graphic acceleration card for computers?

“Discover the force of the heavens O Men:
Once recognised it can be put to use:
No use could be seen in unknown things.”
— Johannes Kepler, De fundamentis astrologiae certioribus [11]

Kepler’s Youth

Johannes Kepler was born on December 27, 1571 in the free imperial city of Weil der Stadt. His father, Heinrich Kepler, earned an insecure living as a trader and left the family several times to serve as a mercenary abroad. His mother Katharina, an innkeeper’s daughter, was an herb woman and was later accused of witchcraft. In 1575 he survived a smallpox disease which, however, permanently impaired his vision. Despite his poor health, he was precocious and often impressed travellers at his mother’s inn with his mathematical skills.

The Heliocentric System

With the acquisition of a scholarship in 1589 Kepler began to study theology at the Evangelical Monastery in Tübingen despite modest family circumstances. He studied with the mathematician and astronomer Michael Mästlin, saw himself as an outstanding mathematician and acquired the reputation of a skilled astrologer. Under the guidance of Michael Mästlin he became acquainted with the heliocentric system of planetary movements of Nicolaus Copernicus.

Meeting Tycho Brahe

Kepler originally wanted to become a Protestant clergyman. In 1594, however, at the age of 23, he accepted a teaching position in mathematics at the Protestant monastery school in Graz. In December 1599 Tycho Brahe invited Kepler to work with him in Prague. Forced by the Counter-Reformation to leave Graz, Kepler met Brahe in 1600.[6] However, Brahe was an excellent observer, but his mathematical skills were limited. The outstanding mathematician Kepler, on the other hand, could hardly make precise observations due to his ametropia. Brahe, however, with his extensive life’s work, the records of astronomical observations of the planetary orbits and hundreds of stars, feared to establish Kepler’s fame alone. In addition, Brahe only partially shared the astronomical views of Kepler (and Copernicus). After Brahe’s death in 1601, Kepler became imperial court mathematician. In October 1604, Kepler observed a supernova that was later called Kepler’s star.[5] Kepler published his observations in 1606 in the book De Stella nova in pede serpentarii, et qui sub ejus exortum de novo iniit, Trigono igneo (‘On the new star at the foot of the snakebearer’). The emergence of this “new” star contradicted the prevailing view that the fixed star vault was eternally unchangeable and triggered fierce discussions among experts in natural philosophy.

Building upon the Results of Brahe

By working with Brahe’s extensive collection of very accurate observational data, Kepler wanted to improve his earlier theories, but had to reject them in view of the measurement data. He then began to design a new astronomical system. Starting from the Copernican system, he determined the real planetary orbits for the first time, without committing himself from the outset that they would have to be a combination of circular orbits run through in a uniform manner. He completed these works in 1606 and published them in 1609 as Astronomia nova. The book contained Kepler’s first and second laws. After intensive study of data on the orbit of Mars, Kepler discovered the third of the laws named after him on 15 May 1618, which he explained in the work Harmonices mundi libri V (“Five Books on the Harmonics of the World“) published in 1619.

“Geometry is one and eternal shining in the mind of God. That share in it accorded to humans is one of the reasons that humanity is the image of God.”
— Johannes Kepler, Harmonices Mundi (1618)

Kepler’s Laws

I’m quite sure you will remember Kepler’s Laws of planetary motion. In astronomy, Kepler’s laws of planetary motion are three scientific laws describing the motion of planets around the Sun. (If not so, here is a brief recollection…):

1. The orbit of every planet is an ellipse with the Sun at one of the two foci.
2. A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.
3. The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.

Most planetary orbits are nearly circular, and careful observation and calculation are required in order to establish that they are not perfectly circular. Calculations of the orbit of Mars, whose published values are somewhat suspect,  indicated an elliptical orbit. From this, Johannes Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits.

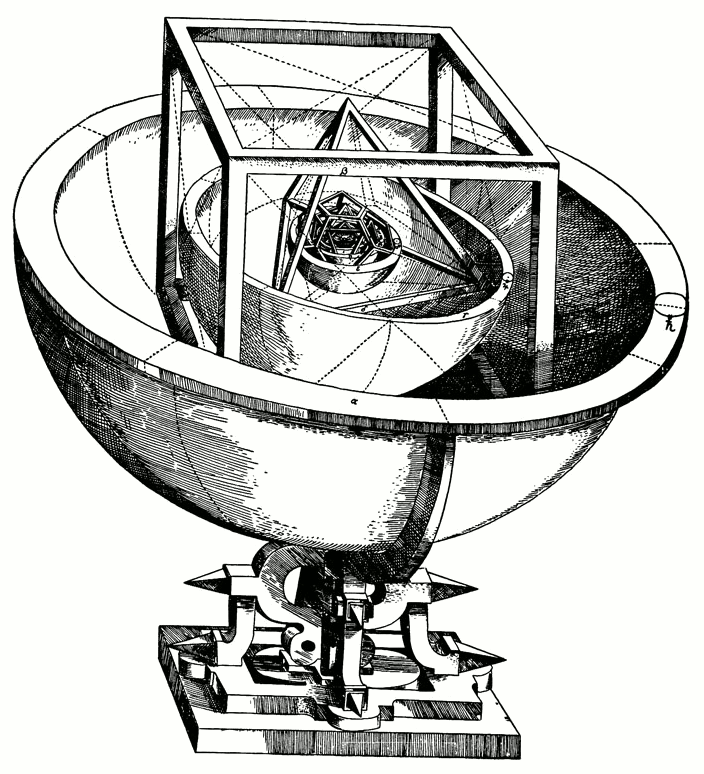
Kepler’s model of the solar system: Mystery Cosmographicum (1596)

Kepler’s Radical Claims

At the time, Kepler’s laws were really radical claims. The prevailing belief was that planetary orbits should be based on perfect circles – at least according to philosophy. Most of the planetary orbits can be rather closely approximated as circles, so it is not immediately evident that the orbits really are ellipses. Detailed calculations for the orbit of the planet Mars first indicated to Kepler its elliptical shape, and he inferred that other heavenly bodies, including those farther away from the Sun, have elliptical orbits too. Kepler’s laws and his analysis of the observations on which they were based, the assertion that the Earth orbited the Sun, proof that the planets’ speeds varied, and use of elliptical orbits challenged the long-accepted geocentric models of Aristotle and Ptolemy, and finally supported the heliocentric theory of Nicolaus Copernicus.

The Harmony of Celestial Spheres

Kepler discovered the laws of the planets by seeking to complete Pythagoras‘ goal of finding the harmony of the celestial spheres. From his cosmological point of view it was no coincidence that the number of regular polyhedra was one smaller than the number of known planets. He tried to prove that the distances of the planets from the sun are given by spheres within regular polyhedra.In his work Harmonice mundi (World Harmonic), published in 1619, he established a connection between the Platonic bodies and the classical conception of the elements, just as he did in the Mysterium Cosmographicum. The tetrahedron was the form of the fire, the octahedron the symbol of the air, the cube the symbol of the earth, the icosahedron symbolized the water and the dodecahedron stood for the cosmos as a whole or the ether.

Astrology on a Safe Basis?

Kepler was convinced that certain constellations of celestial bodies could influence man like the weather. He tried to fathom the connections and wanted to put astrology on a scientific basis. In his 1601 publication De Fundamentis Astrologiae Certioribus (“On More Reliable Foundations of Astrology“), Kepler set out how astrology could be practiced on a safe basis by applying it to new scientific knowledge in connection with the Pythagorean idea of world harmony. This too was an affront to his conservative contemporaries who preferred Ptolemaic astronomy.

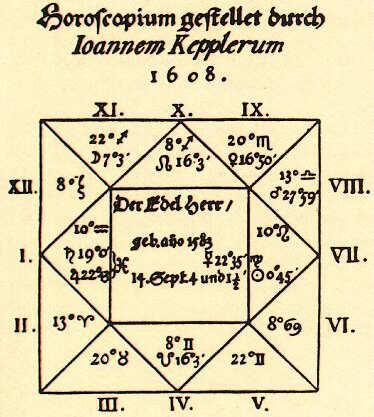
Kepler’s first horoscope for Wallenstein from 1608

A Life in Turmoil

From 1615 Kepler had to take care of the defense of his mother Katharina, who was imprisoned under the suspicion of witchcraft. In a character in Kepler’s novel Somnium (“The Dream“), which describes a magical journey to the moon, the prosecution said it recognizes Kepler’s mother. In October 1621 he obtained her release. The problems accumulated in Linz. Kepler had trouble collecting his money claims. The family had to fly to Ulm. n 1627 Kepler found a new patron in the imperial General Albrecht von Wallenstein.[7] He expected reliable horoscopes from Kepler and in return made a print shop available in Sagan (Silesia). However, when Wallenstein lost his function as commander-in-chief at the Reichstag in Regensburg in August 1630, Kepler travelled to Regensburg to claim outstanding salary claims of 12,000 guilders at the Reichstag. After a short stay in Regensburg, Kepler fell seriously ill and died on November 15, 1630 at the age of 58.

Isaac Newton showed in 1687 that relationships like Kepler’s would apply in the Solar System to a good approximation, as a consequence of his own laws of motion and law of universal gravitation.

The composer Paul Hindemith set Kepler a musical monument with his opera The Harmony of the World, completed in 1957, that is baed in Johannes Kepler’s biography.

R. Shankar, 7. Kepler’s Laws, [12]

• [1] Nicolaus Copernicus and the Heliocentric Model, SciHi Blog
• [2] Works by Johannes Kepler at Project Gutenberg
• [3] Harmonices mundi (“The Harmony of the Worlds”) in fulltext facsimile; Carnegie-Mellon University
• [4] Liscia, Daniel A. Di. “Johannes Kepler“. In Zalta, Edward N. Stanford Encyclopedia of Philosophy.
• [5] Much More Powerful Than Expected – Kepler’s Supernova, SciHi Blog
• [6] Tycho Brahe – The Man with the Golden Nose, SciHi Blog
• [7] The Assassination of Wallenstein, SciHi Blog
• [8] Johannes Kepler at Wikidata
• [9] Christmas Trilogy 2015 Part 3: Roll out the barrel., The Renaissance Mathematicus, December 27, 2015.
• [10] Kepler’s divine geometry. The Renaissance Mathematicus, November 15, 2010.
• [11] Johannes Kepler, De fundamentis astrologiae certioribus [On the more Certain Fundamentals of Astrology or On Giving Astrology Sounder Foundations] (written 1601; published 1602) in Opera Omnia, Vol. 1, Heyder & Zimmer, 1858, p. 417 (title-page)
• [12] R. Shankar, 7. Kepler’s Laws, Fundamentals of Physics (PHYS 200), Yale Courses @ youtube
• [13] Steven N. Shore, Václav Pavlík, How a fake Kepler portrait became iconic, Physics Today 74, 9, 10 (2021); https://doi.org/10.1063/PT.3.4825
• [14] Timeline for Johannes Kepler, via Wikidata