
Vito Volterra (1860-1940)
On May 3, 1860, Italian mathematician and physicist Vito Volterra was born. He is known for his contributions to mathematical biology and integral equations. Moreover, he is considered as one of the founders of functional analysis.
“Empires die, but Euclid’s theorems keep their youth forever” — Vito Volterra
Youth and Education
Vito Volterra was born in Ancona, then part of the Papal States, as son of Abramo Volterra, a cloth merchant, into a very poor Jewish family. Actually, Volterra was born at exactly the time (May 1860) when Giuseppe Garibaldi set out to conquer Sicily and Naples and so to create a unified Italy. His father Abramo died when Vito was only two years old, and the family was left without any means of financial support. They only survived because a brother of Vito’s mother, took care of them.Volterra showed early promise in mathematics, but since his family were extremely poor, there was pressure to take a job. However, his determination to continue studying, supported by his uncle Edoardo, saw him continue. At the age of 13, he was already dealing with the three-body problem. Two of his former teachers at the Galileo Galilei Technical Institute, Cesare Arzelà and Antonio Ròiti quickly realised that Vito was an extremely talented mathematician and offered him further support. Ròiti offered Vito a position teaching physics at the Istituto di Studi Superiori e di Perfezionamento in Florence in 1877, and thus, Volterra was able to proceed to the University of Pisa in the autumn of 1878, enrolling in the faculty of Science, where scored the highest possible marks and received a scholarship together with free board and lodgings. At Pisa he worked for his thesis advised by Enrico Betti, graduating with his laurea in 1882 with a thesis on hydrondynamics, and there became professor of rational mechanics in 1883.[1]
The Theory of Functionals
Volterra immediately started work developing his theory of functionals, i.e. functions that depend on a continuous set of values of another function. This concept led to the development of new fields of analysis, including important applications to the solution of integral and differential equations. The important idea of harmonic integrals derives essentially from his functional calculus. He also applied his analytic methods with good results to optics, electromagnetism, and elasticity and to the theory of distortions.[2] His work is summarized in his book Theory of functionals and of Integral and Integro-Differential Equations (1930).
Dislocations in Crystals
In 1892, Volterra became professor of mechanics at the University of Turin and then, in 1900, professor of mathematical physics at the University of Rome La Sapienza. In 1905, king Victor Emmanuel III made him a senator of the Kingdom of Italy in 1905. In the same year, he began to develop the theory of dislocations in crystals that was later to become important in the understanding of the behavior of ductile materials. On the outbreak of World War I, although already 55 years of age, Volterra joined the Italian Air Force and worked on the development of dirigible airships under Giulio Douhet. He originated the idea of using inert helium rather than flammable hydrogen in airships and helped organize helium manufacture in Italy.
Mathematical Models of Biological Systems
After World War I, Volterra turned his attention to the application of his mathematical ideas to biology, principally reiterating and developing the work of Pierre François Verhulst. Unknown to him, much of his work duplicated that of previous researchers, but it drew the attention of mathematicians to the field. His abstract mathematical models of biological processes (such as predator-prey systems) found many analogies in physical science. The most famous outcome of this period is the Lotka–Volterra equations, which have been found independently by Volterra and the Austrian mathematician Alfred J. Lotka in 1925/26. These are mathematical differential equations in which the quantitative aspect of population development as a function of time was presented for the first time. They are based on the logistic equation. The biological applications of these equations are known today under the names of the first, second and third Lotka-Volterra rule.
The Predator-Prey Model
“I did not hesitate at the Congress of Mathematicians at Paris to call the nineteenth century the century of the theory of functions, as the eighteenth century might have been called that of infinitesimal calculus.”
– Vito Volterra, as quoted in [12]
In the Lotka-Volterra model, predator and prey species show coupled frequency fluctuations. A rich supply of food and prey enables predators to raise many offspring so that the predator population grows. The greater population density of predators leads to a decimation of the prey population and thus to a deficient food supply for predators, so that fewer or no young animals can be raised and weak adult predators starve to death. This decline in the predator population now allows the prey population to recover and the periodical process starts all over again.
In the model, however, these are so-called neutrally stable cycles. This means: The cycles are created without external influences, the cycle length results from the choice of variables (without timer), without external disturbances these cycles would continue forever without any deviation. But: In natural systems actually observable cycles cannot normally develop due to this mechanism, due to the inevitable and always acting fluctuations of the environmental variables populations, which are subject to the model dynamics, would fluctuate in reality acyclically and erratically. Populations whose fluctuations could be explained solely by the model probably do not exist. Nevertheless, the model is useful as a first approximation to explain coupled fluctuations in population density.
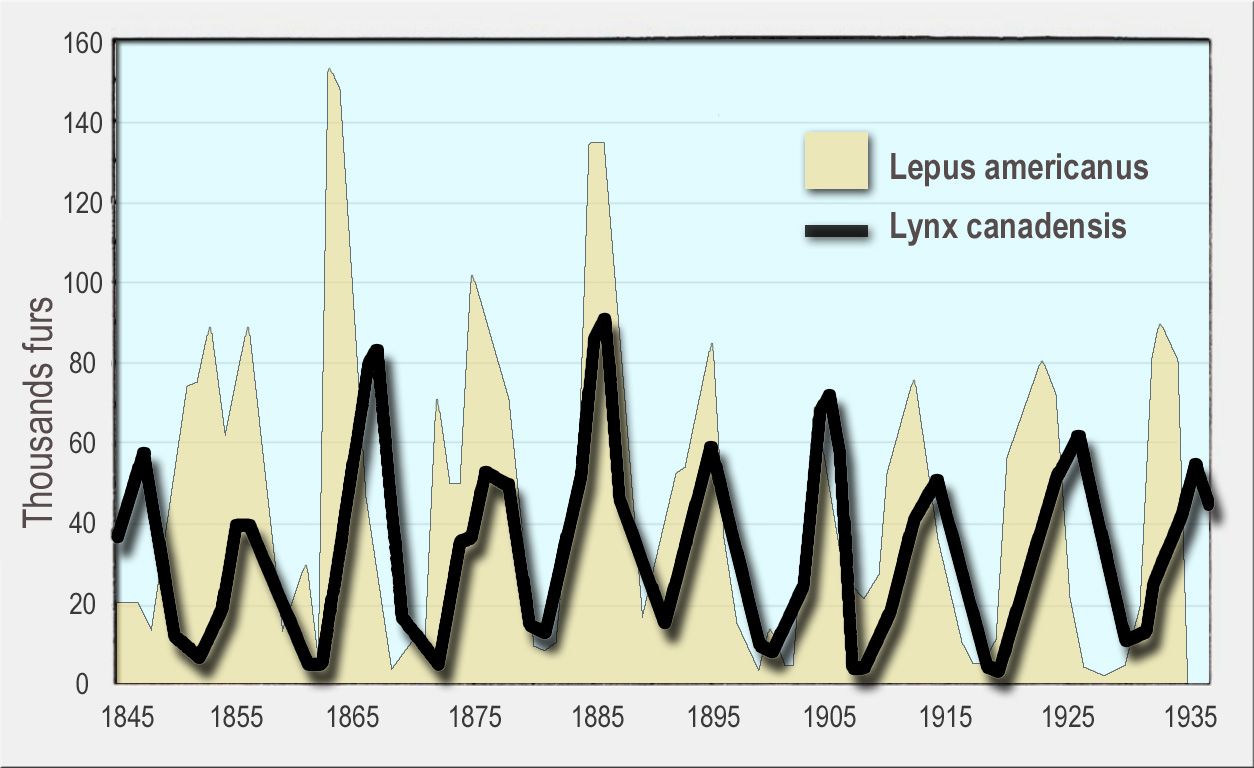
Numbers of snowshoe hare (yellow, background) and Canada lynx (black line, foreground) furs sold to the Hudson’s Bay Company. Canada lynxes eat snowshoe hares.
In Opposition to the Facists
In 1922, Volterra joined the opposition to the Fascist regime of Benito Mussolini, who came to power in 1923 although at this time the Facists did not adopt racial policies. However in 1931 Volterra was one of only 12 out of 1,250 professors who refused to take a mandatory oath of loyalty to the Facist government. As a result of his refusal to sign the oath of allegiance to the fascist government he was compelled to resign his university post and all his membership of scientific academies, and, during the following years, he lived largely abroad, returning to Rome just before his death in 1940.
Dr. Sandra Linguerri Technion Lecture about Vito Volterra, [11]
References and Further Reading:
- [1] O’Connor, John J.; Robertson, Edmund F., “Vito Volterra“, MacTutor History of Mathematics archive, University of St Andrews.
- [2] Vito Volterra at Encyclopedia Britannica
- [3] God made the integers, all the rest is the work of man – Leopold Kronecker, SciHi Blog
- [4] Richard Dedekind and the Real Numbers, SciHi Blog
- [5] Carl Friedrich Gauss – The Prince of Mathematicians, SciHi Blog
- [6] Emmy Noether and the Love for Mathematics, SciHI Blog
- [7] Vito Volterra at zbMATH
- [8] Vito Volterra at Mathematics Genealogy Project
- [9] Vito Volterra at Electronic Research Archive for Mathematics Jahrbuch Database
- [10] Vito Volterra at Wikidata
- [11] Dr. Sandra Linguerri Technion Lecture about Vito Volterra, Symposium sponsored by the Italian Technion Association, May 1, 2013., Technion @ youtube
- [12] Griffith Conrad Evans: Henri Poincaré. 1. May 1915. 133–162. (quote from p. 140)
- [13] Castelnuovo, G. (1943), “Vito Volterra”, Rendiconti della Accademia Nazionale delle Scienze Detta dei XL, Memorie di Matematica e Applicazioni, Serie 3 (in Italian), XXV (70): 87–95
- [14] Goodstein, Judith R. (2007), The Volterra Chronicles: The Life and Times of an Extraordinary Mathematician 1860–1940, History of Mathematics, vol. 31, Providence, RI–London: American Mathematical Society/London Mathematical Society,
- [15] Timeline for Vito Volterra, via Wikidata





