
Edward Norton Lorenz (1917-2008)
On May 23, 1917, American mathematician, meteorologist, and a pioneer of chaos theory Edward Norton Lorenz was born. He is best known for pointing out the “butterfly effect” whereby chaos theory predicts that “slightly differing initial states can evolve into considerably different states.” In his 1963 paper in the Journal of Atmospheric Sciences, he cited the flapping of a seagull‘s wings as changing the state of the atmosphere in even such a trivial way can result in huge changes in outcome in weather patterns.
“Mathematicians seem to have no difficulty in creating new concepts faster than the old ones become well understood, and there will undoubtedly always be many challenging problems to solve. nevertheless, I believed that some of the unsolved meteorological problems were more fundamental, and I felt confident that I could contribute to some of their solutions.”
– Edward Lorentz (1991) “A scientist by choice”. Speech by acceptance of the Kyoto Prize
Edward Lorenz – Early Years
Edward Lorenz was born in West Hartford, Connecticut. After receiving degrees from Dartmouth College and Harvard University in mathematics, Lorenz turned to weather forecasting in 1942 with the U.S. Army Air Corps, where he involved applying his mathematical skills to weather forecasting and soon he was looking to undertake further study of meteorology.[2] After World War II he decided to became a researcher at the Massachusetts Institute of Technology, where he earned a master’s degree (1943) and doctorate in meteorology (1948) after submitting the dissertation A Method of Applying the Hydrodynamic and Thermodynamic Equations to Atmospheric Models. Lorenz spent his whole career at the Massachusetts Institute of Technology, being appointed assistant professor in 1954, then promoted to associate professor before becoming Professor of Meteorology in 1962. He served as Head of Department from 1977 to 1981, retiring in 1987 when he was made professor emeritus.[2]
Non-linear statistical Models for Meteorology
During the 1950s, Lorenz became skeptical of the appropriateness of the linear statistical models in meteorology, as most atmospheric phenomena involved in weather forecasting are non-linear. His work on the topic culminated in the publication of his 1963 paper “Deterministic Nonperiodic Flow” in Journal of the Atmospheric Sciences, and with it, the foundation of chaos theory. He constructed a weather model showing that almost any two nearby starting points, indicating the current weather, will quickly diverge trajectories and will quite frequently end up in different “lobes,” which correspond to calm or stormy weather. He explained this phenomenon, which makes long-range weather forecasting impossible, to the public as the “butterfly effect”: in China a butterfly flaps its wings, leading to unpredictable changes in U.S. weather a few days later.[1] In chaos theory, the butterfly effect is the sensitive dependence on initial conditions in which a small change in one state of a deterministic nonlinear system can result in large differences in a later state.
The Butterfly Effect
Lorenz had discovered the effect by chance. One day in 1961, he wanted to repeat one of his weather simulations using a simple computer model for a longer time, but instead of repeating the whole simulation, he started the second run in the middle, typing in numbers from the first run for the initial conditions. The computer program was the same, so the weather patterns of the second run should have exactly followed those of the first. Instead, the two weather trajectories quickly diverged on completely separate paths, simply because Lorenz had made a small rounding error with his inputs of less then 0.1 percent — he entered the initial condition 0.506 from the printout instead of entering the full precision 0.506127 value — which completely changed the end result. Lorenz soon realized that this meant perfect weather prediction was nothing but a fantasy.[3] The butterfly effect presents an obvious challenge to prediction, since initial conditions for a system such as the weather can never be known to complete accuracy.
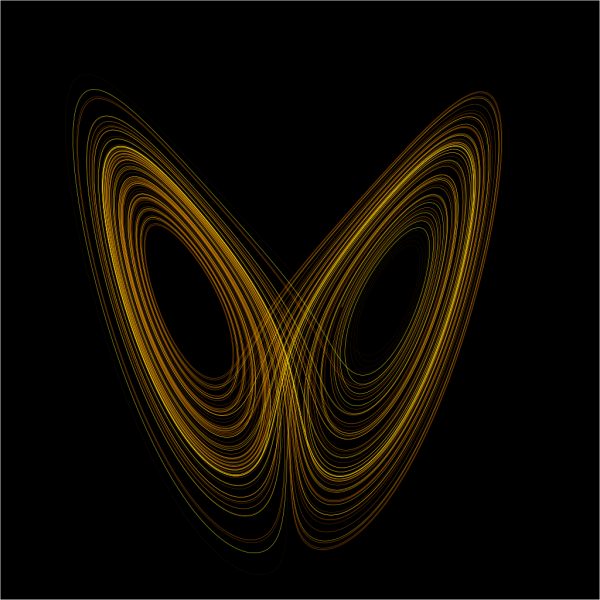
A plot of Lorenz’s strange attractor for values ρ=28, σ = 10, β = 8/3.
Chaos Theory and Lorenz Attractor
Edward Lorenz was not the first person to discover chaos.[2] Chaos theory and the sensitive dependence on initial conditions were described in the literature in a particular case of the three-body problem by Henri Poincaré in 1890, who later proposed that such phenomena could be common, for example, in meteorology.[4] However, Poincaré’s discovery had not led to any significant developments. Lorenz’s 1963 paper, like Poincaré’s work 80 years earlier, had relatively little impact in the time immediately after it appeared. However, it has gone on to become one of the most quoted papers of all time. The set of equations and the attractors described by this set of equations are now called the Lorenz equations and Lorenz attractors, respectively. It would be fair to say that Edward Lorenz began a scientific revolution with this paper which he and many others developed over the following years. In 1972 he addressed the American Association for the Advancement of Science giving a talk with the title Predictability: Does the Flap of a Butterfly’s Wings in Brazil Set off a Tornado in Texas? By encapsulating the essence of chaos theory in the title of his talk, Lorenz succeeded in capturing the public’s imagination and the term “butterfly effect” was soon the popular term for chaos.
Honors
Edward Lorenz, who was elected to the National Academy of Sciences in 1975, won numerous awards, honors as well as honorary degrees. In 1983, he and former MIT Professor Henry M. Stommel were jointly awarded the $50,000 Crafoord Prize by the Royal Swedish Academy of Sciences, a prize established to recognize fields not eligible for Nobel Prizes. Edward Lorenz died on April 16, 2008 in Cambridge, Massachussetts, at age 90.
Chaos | Chapter 7 : Strange Attractors – The butterfly effect, [9]
References and Further Reading:
- [1] Edward Lorenz, American meteorologist and mathematician, at Britannica Online
- [2] O’Connor, John J.; Robertson, Edmund F., “Edward Norton Lorenz”, MacTutor History of Mathematics archive, University of St Andrews.
- [3] Kenneth Chang: Edward N. Lorenz, a Meteorologist and a Father of Chaos Theory, Dies at 90, The New York Times, April 17, 2008.
- [4] Henri Poincaré – the Last Universalist of Mathematics, SciHi blog, April 29, 2014.
- [5] Edward Norton Lorenz at Wikidata
- [6] Obituary, Daily Telegraph, 18 April 2008.
- [7] Palmer, T. N. (2009). “Edward Norton Lorenz. 23 May 1917 — 16 April 2008”. Biographical Memoirs of Fellows of the Royal Society. 55: 139–155.
- [8] Edward Lorenz, father of chaos theory and butterfly effect, dies at 90″. MIT Tech Talk. 2008-04-30.
- [9] Chaos | Chapter 7 : Strange Attractors – The butterfly effect, It’s so blatant @ youtube
- [10] Timeline of Chaos Theorists, via DBpedia and Wikidata






Pingback: Whewell’s Gazette: Year 03, Vol. #41 | Whewell's Ghost