
Archytas of Tarentum (428-347 BC), from Mathematicians and astronomers: twenty portraits. Engraving by J.W. Cook, 1825.
At about 428 BC, Ancient Greek philosopher, mathematician, astronomer, statesman, and strategist Archytas of Tarentum was born. A scientist of the Pythagorean school he is famous for being the reputed founder of mathematical mechanics, as well as a good friend of Plato.
“That tho’ a Man were admitted into Heaven to view the wonderful Fabrick of the World, and the Beauty of the stars, yet what would otherwise be Rapture and Extasie, would be but melancholy Amazement if he had not a Friend to communicate it to.”
— Attributed to Archytus by Christiaan Huygens, The Celestial Worlds Discover’d (1722)
Archytas of Tarentum
Archytas was born in Tarentum, Magna Graecia, an area on the heel of the boot of Italy which was under Greek control in the 5th century BC, and was the son of Mnesagoras or Histiaeus. For a while, he was taught by Philolaus, a student of Pythagoras who, after Pythagoras died, fled to Lucania and then to Thebes in Greece. He returned to Italy where he taught Archytas. Archytas was a teacher of mathematics to Eudoxus of Cnidus [2]. As a Pythagorean, Archytas believed that only arithmetic, not geometry, could provide a basis for satisfactory proofs. Interestingly, Archytas is counted as pre-socratic philosopher, although there must have been an exchange of letters between Plato, i.e. Socrates’ student, and Archytas. Actually, Archytas sent a ship to rescue Plato from the clutches of the tyrant of Syracuse, Dionysius II, in 361 BC.[3] This classification, however, is because of the style of Archytas’ philosophy rather than the strict chronology.[1]
Only Fragments tell us about his Life
Apart from the surviving fragments of his writings, our knowledge of Archytas’ life and work depends heavily on authors who wrote in the second half of the fourth century, in the fifty years after Archytas’ death. Archytas’ importance both as an intellectual and as a political leader is reflected in the number of writings about him in this period, although only fragments of these works have been preserved.[3]
A Pythagorean and a Flying Device
Although Archytas studied many topics, since he was a Pythagorean, mathematics was his main subject and all other disciplines were seen as dependent on mathematics.[1] Archytas is believed to be the founder of mathematical mechanics. As only described in the writings of Aulus Gellius five centuries later, he was reputed to have designed and built the first artificial, self-propelled flying device, a bird-shaped model propelled by a jet of what was probably steam, said to have actually flown some 200 meters. This machine, which its inventor called The pigeon, may have been suspended on a wire or pivot for its flight. Another mechanical device invented by Archytas was a rattle for children which was useful, in Aristotle’s words
“… to give to children to occupy them, and so prevent them from breaking things about the house (for the young are incapable of keeping still).” (T L Heath, A History of Greek Mathematics (2 Vols.) (Oxford, 1921))
Lost Works
Archytas also wrote some lost works, as he was included by Vitruvius in the list of the twelve authors of works of mechanics. Archytas named the harmonic mean, important much later in projective geometry and number theory, though he did not invent it. According to Eutocius, Archytas was the first to solve one of the most celebrated mathematical problems in antiquity, the duplication of the cube. He did it in his manner with the help of a geometric construction. Hippocrates of Chios before, reduced this problem to finding mean proportionals. He saw the ultimate goal of the sciences as the description of individual things in the world in terms of ratio and proportion and accordingly regarded logistic, the science of number and proportion, as the master science [3].
The Universe is Unlimited in Size
Archytas also developed a rather famous argument to show that the universe is unlimited in size: He asks anyone who argues that the universe is limited to engage in a thought experiment: “If I arrived at the outermost edge of the heaven, could I extend my hand or staff into what is outside or not? It would be paradoxical [given our normal assumptions about the nature of space] not to be able to extend it.” The end of the staff, once extended will mark a new limit. Archytas can advance to the new limit and ask the same question again, so that there will always be something, into which his staff can be extended, beyond the supposed limit, and hence that something is clearly unlimited.[3]
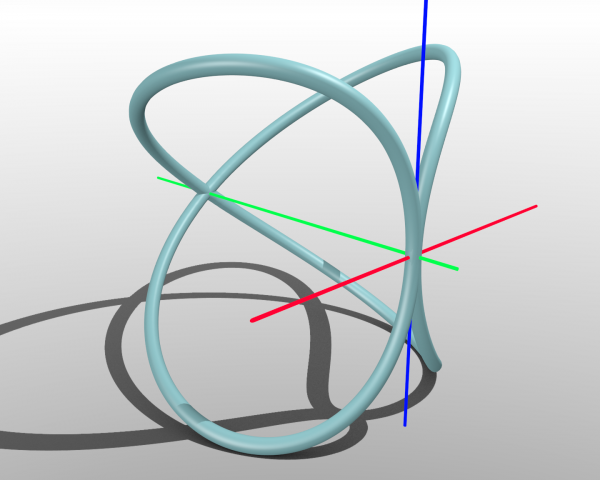
An Archytas curve, an intersection of a torus and a cylinder.
The Archytas Curve
Archytas’ theory of proportions is treated in book VIII of Euclid’s Elements, where is the construction for two proportional means, equivalent to the extraction of the cube root. According to Diogenes Laertius, this demonstration, which uses lines generated by moving figures to construct the two proportionals between magnitudes, was the first in which geometry was studied with concepts of mechanics. The Archytas curve, which he used in his solution of the doubling the cube problem, is named after him. The Archytas curve is created by placing a semicircle (with a diameter of d) on the diameter of one of the two circles of a cylinder (which also has a diameter of d) such that the plane of the semicircle is at right angles to the plane of the circle and then rotating the semicircle about one of its ends in the plane of the cylinder’s diameter. This rotation will cut out a portion of the cylinder forming the Archytas curve.
Political Life
Politically and militarily, Archytas appears to have been the dominant figure in Tarentum. The Tarentines elected him strategos, ‘general’, seven years in a row – a step that required them to violate their own rule against successive appointments. In his public career, Archytas had a reputation for virtue as well as efficacy. Some scholars have argued that Archytas may have served as one model for Plato’s philosopher king, and that he influenced Plato’s political philosophy as expressed in The Republic and other works.
Archytas’ Steam Powered Pigeon – Steam Culture, [8]
References and Further Reading:
- [1] O’Connor, John J.; Robertson, Edmund F., “Archytas“, MacTutor History of Mathematics archive, University of St Andrews.
- [2] Eudoxus and the Method of Exhaustion, SciHi blog.
- [3] Huffman, Carl. “Archytas“. Stanford Encyclopedia of Philosophy.
- [4] Laërtius, Diogenes (1925). “Pythagoreans: Archytas“. Lives of the Eminent Philosophers 2:8.
- [5] Fragments of Archytas and Life of Archytas at Demonax, Hellenic Library
- [6] Archytas at Wikidata
- [7] Original works written by or about Archytas at Wikisource
- [8] Archytas’ Steam Powered Pigeon – Steam Culture, wareboilers @ youtube
- [9] von Fritz, Kurt (1970). “Archytas of Tarentum“. Dictionary of Scientific Biography. Vol. 1. New York: Charles Scribner’s Sons. pp. 231–233.
- [10] Timeline of Pythagoreans, via DBpedia and Wikidata





